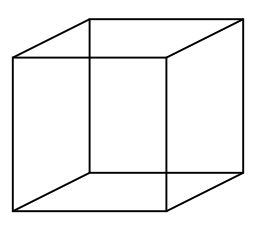
The creation of Impossible Cube is often attributed to the Dutch artist M.C. Escher. The illusion is based on the Necker Cube, which was first described in 1832 by the Swiss crystallographer Louis Albert Necker. Necker noticed that cubes as well as other rhomboids when drawn as wireframes with no cues to depth or orientation could appear to be in two possible orientations. The impossible cube makes use of this effect, often called metastable perception, by including parts of both possible orientations to create a contradictory cube.
Above is one possible way of making an impossible cube, where the edges of the cube that would be closest to the viewer are cut from the viewer’s perspective to reveal the back edges, giving the illusion that they are in front of the closer edges. Even though they are cut, the closer edges still appear to be continuous as they are aligned. Earlier in the 1920’s a group of German psychologists, most notably Max Wertheimer and Wolfgang Köhler, proposed a set of principles that tried to explain related perceptual phenomena. These principles, known as the Gestalt Principles, are commonly known as similarity, continuation, closure, proximity, figure/ground, and symmetry/order (also known as prägnanz). The perceived continuity in the above impossible cube follows the Continuity principle, where objects that seemingly follow the same line are more likely to appear connected to one another.